Imposing Average Homogenization Constraints with the Lagrangian Kernels
Purpose of the Homogenization System
The homogenization system is a means to impose cell-average stress or strain conditions on periodic unit cell models using the new, Lagrangian kernels and specifically the total Lagrangian formulation. These types of constraints are very useful for homogenization simulations trying to determine the effective mechanical properties of a representative volume of material.
Mathematical Description
Danielsson et al. (2002) describes the theory underlying the homogenization system. The system aims to impose cell average stress or deformation constraints. For small deformations these constraints are of the type or and for large deformations the constraint options are: or The "hat" quantities are targets set by the user with a MOOSE Function. These targets control the cell-average stress or strain. For large deformations the system imposes the constraints on the 1st Piola-Kirchhoff stress or the displacement gradient. For small deformations the system constrains the small stress or the small strain. As with the underlying kernels, the system uses the large_kinematics flag to switch between small and large deformation theory. Components can be mixed and matched – the system can impose deformation constraints in one tensor direction and stress constrains in the others. The number of available constraints varies by the problem dimension and the kinematic theory. Table 1 lists the available number of constraints and the order in which they appear when specified in the input file. The small kinematic theory admits fewer constraints because the relevant stress and strain tensors are symmetric. The small deformation constraints unroll following the Voigt convention, the large deformation constraints are the row-major unrolled full tensor
Table 1: Number of available constraints and input file order
| Problem dimension | Small deformation constraints | Large deformation constraints |
|---|---|---|
| 1 | 1: | 1: |
| 2 | 3: , , | 4: , , , |
| 3 | 6: , , , , | 9: , , , , , , , , |
To meet these cell average stress or strain components the system introduces an extra, affine displacement field over the domain where is the interpolated displacement field arising from the standard finite element problem and for some constant gradient tensor . For small deformations the gradient tensor is symmetric, for large deformations it is not. In either case, the system adds this extra gradient to the deformation gradient calculated from the micro displacement field before forming the strain measures and calculating the resulting stress. The framework represents the constant field with a MOOSE scalar variable.
The system implements the constrains by imposing a scalar residual equation for each specificed constraint: where represents a stress or deformation constrain, as appropriate. This constraint is implemented as a ScalarKernel. using a UserObject to visit each element and compute the volume integral.
Example Simulation
Figure 1 shows a simple, but representative, sample simulation. It consists of a square, 2D simulation cell subdivided into four subdomain. The material model in each subdomain is a St. Venant-Kirchhoff model, but the material properties in each subdomain are different as indicated on the figure. The problem imposes a combination of deformation gradient and 1st Piola Kirchhoff constraints on the simulation cell.
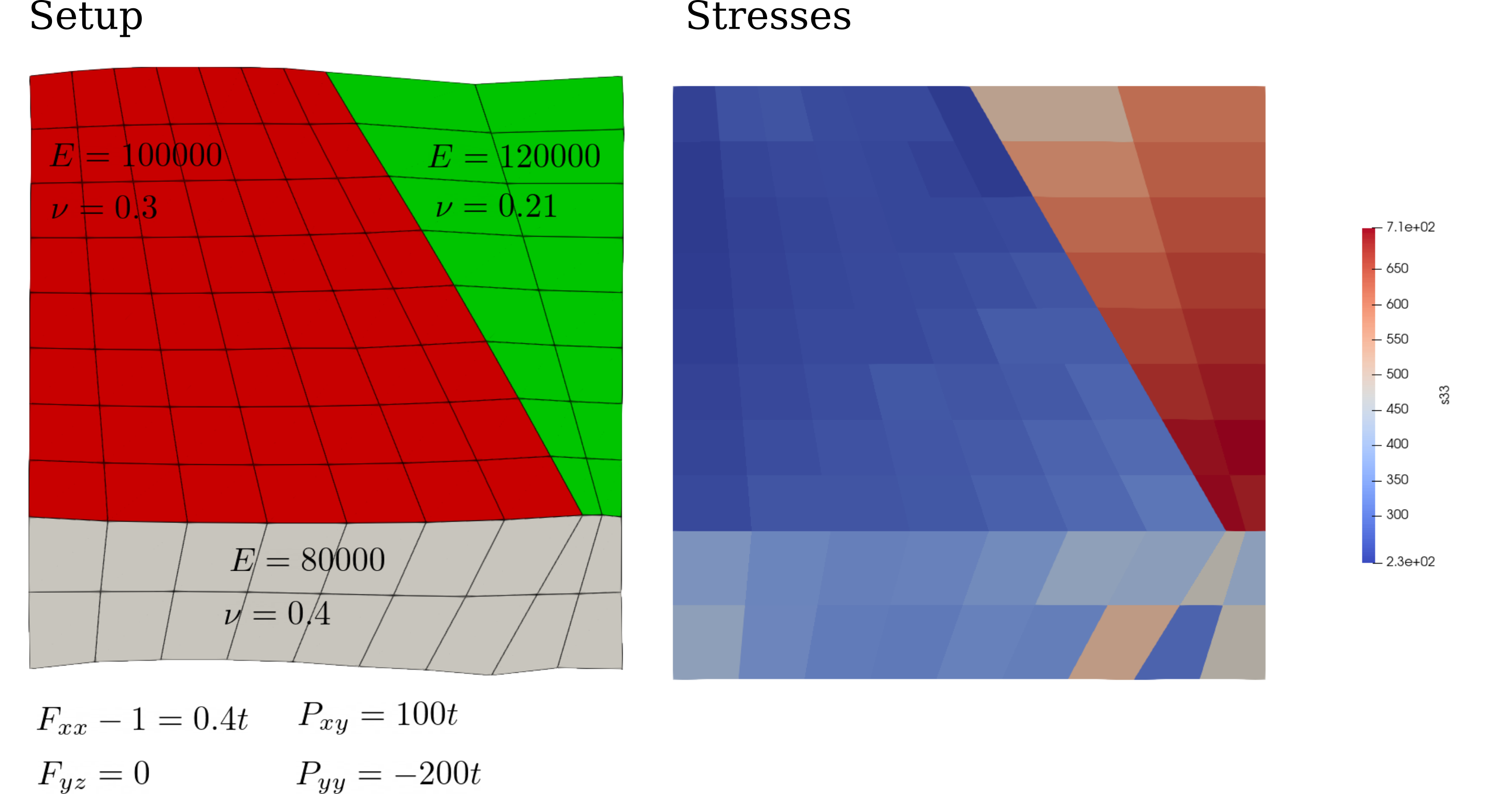
Figure 1: Simple, 2D large deformation homogenization cell problem.
Figure 2 and Figure 3 illustrate that the cell average stress and strain match the constraints for the controlled components of the 1st Piola-Kirchhoff and deformation gradient tensor. The uncontrolled components can vary to maintain equilibrium in the body. Because each subdomain has different material properties the microdisplacements are not homogeneous, producing an inhomogeneous stress state in the simulation cell.
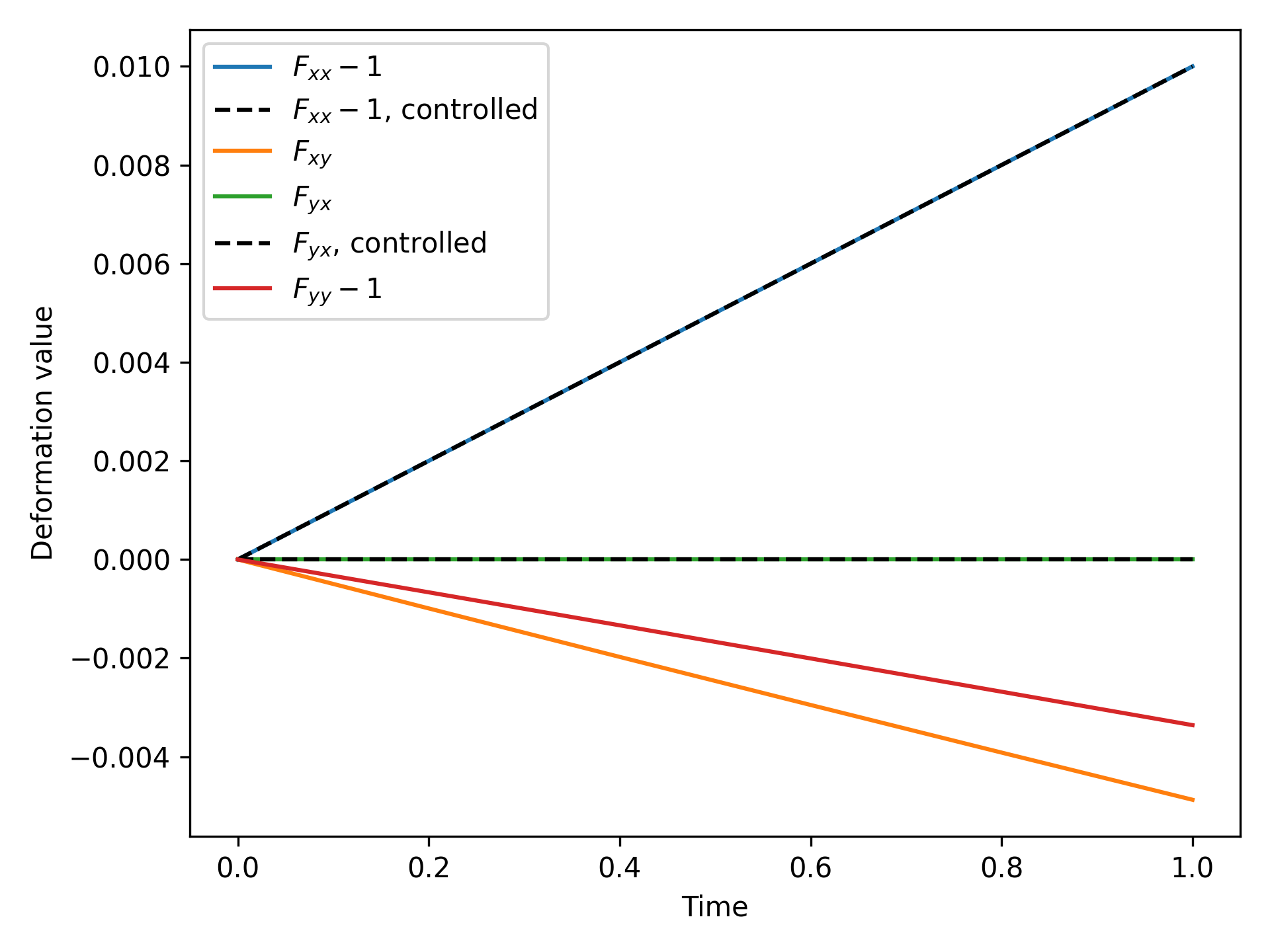
Figure 2: Results showing that the controlled deformation values match their targets.
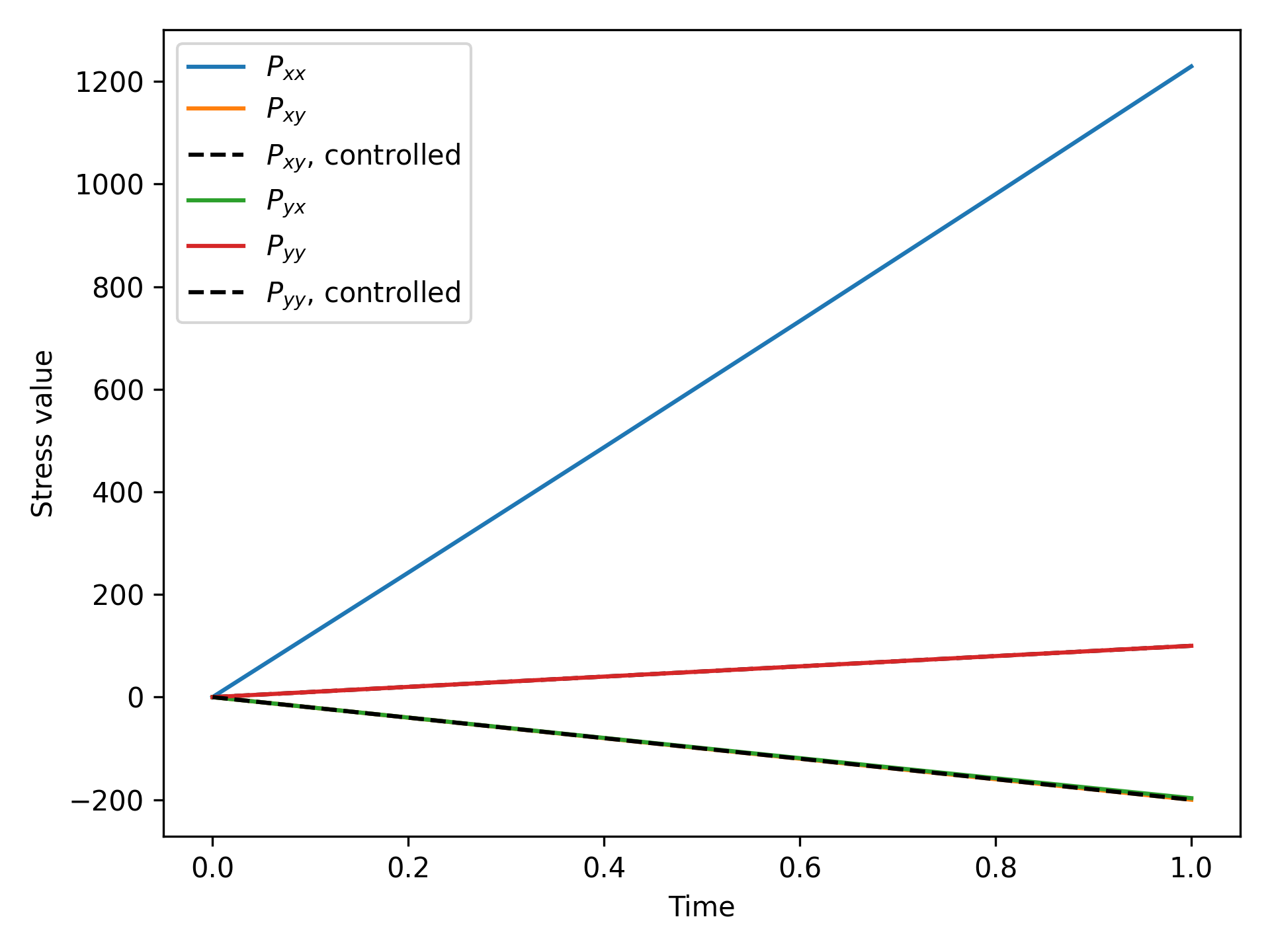
Figure 3: Results showing that the controlled stress values match their targets.
The homogenization system works for 1D, 2D, and 3D problems and for any material model.
Implementation and Requirements
The homogenization system relies on several different objects to impose the constraint residual, specify the constraints, and add the appropriate off-diagonal Jacobian terms. The easiest way to set up a homogenization problem is to use the TensorMechanics/MasterAction which automatically configures the correct MOOSE objects.
The homogenization constraint system only works with the total Lagrangian implementation of the stress equilibrium kernel. Specifically, you must use the HomogenizedTotalLagrangianStressDivergence subclass as it implements the correct off-diagonal Jacobian entries.
The basic requirements the user must setup before imposing the homogenization constraints are:
Setup the unconstrained problem up to the specification of boundary conditions.
Impose periodic boundary conditions on the simulation domain in all directions, using the AddPeriodicBCAction.
Add Dirichlet boundary conditions to constrain the rigid body modes. How to do this will be problem dependent, however a typical method is to constrain 1 (1D), 2 (2D) or 3 (3D) individual nodes with enough Dirichlet conditions to remove the rigid translation and rotation modes.
These actions are not automatically taken care of by the action. At this point the problem should run (i.e. be well-posed with sufficient constraint to solve the stress equilibrium equations) but produce zero deformation or loading.
The final step the user must take is to define their constraints using MOOSE Functions.
For large deformation problems in 2D and 3D the user must specify at least 1 off-diagonal displacement constraint (2D) and at least 3 off-diagonal displacement gradient constraints (3D). That is, not all of the constraints can be stress constraints for large deformations. An unconstrained displacement gradient admits free rigid body rotation and these modes must removed.
The following steps then provide the homogenization constraints. These steps can be replaced by the appropriate options in the TensorMechanics/MasterAction.
Add a
ScalarVariablewith the appropriate order for the problem being solved (see Table 1).Add a
HomogenizationConstraintUserObjectto calculate the volume-averaged constraint value.Add a
HomogenizationConstraintScalarKernelto enforce the constraints.Add a
ComputeHomogenizedLagrangianStrainmaterial object to convert the values of the scalar variable to the homogenization strain or displacement gradient.Inform the
ComputeLagrangianStrainobject of the name of the homogenization strain with thehomogenization_gradient_namesparameter.Use
HomogenizedTotalLagrangianStressDivergencekernels and inform the kernels of the constraints so that they can include the appropriate off-diagonal Jacobian entries with themacro_gradient, andconstraint_typesparameters.
References
- M Danielsson, DM Parks, and MC Boyce.
Three-dimensional micromechanical modeling of voided polymeric materials.
Journal of the Mechanics and Physics of Solids, 50(2):351–379, 2002.[BibTeX]